Dalam Ilmu komputer, Sistem operasi atau dalam bahasa Inggris: operating system atau OS adalah perangkat lunak sistem yang bertugas untuk melakukan kontrol dan manajemen perangkat keras serta operasi-operasi dasar sistem, termasuk menjalankan software aplikasi seperti program-program pengolah kata dan browser web.
Secara umum, Sistem Operasi adalah software pada lapisan pertama yang ditaruh pada memori komputer pada saat komputer dinyalakan. Sedangkan software-software lainnya dijalankan setelah Sistem Operasi berjalan, dan Sistem Operasi akan melakukan layanan inti umum untuk software-software itu. Layanan inti umum tersebut seperti akses ke disk, manajemen memori, skeduling task, dan antar-muka user. Sehingga masing-masing software tidak perlu lagi melakukan tugas-tugas inti umum tersebut, karena dapat dilayani dan dilakukan oleh Sistem Operasi. Bagian kode yang melakukan tugas-tugas inti dan umum tersebut dinamakan dengan “kernel” suatu Sistem Operasi.
Biasanya, istilah Sistem Operasi sering ditujukan kepada semua software yang masuk dalam satu paket dengan sistem komputer sebelum aplikasi-aplikasi software terinstall. Dalam Ilmu komputer, Sistem operasi atau dalam bahasa Inggris: operating system atau OS adalah perangkat lunak sistem yang bertugas untuk melakukan kontrol dan manajemen perangkat keras serta operasi-operasi dasar sistem, termasuk menjalankan software aplikasi seperti program-program pengolah kata dan browser web.
Secara umum, Sistem Operasi adalah software pada lapisan pertama yang ditaruh pada memori komputer pada saat komputer dinyalakan. Sedangkan software-software lainnya dijalankan setelah Sistem Operasi berjalan, dan Sistem Operasi akan melakukan layanan inti umum untuk software-software itu. Layanan inti umum tersebut seperti akses ke disk, manajemen memori, skeduling task, dan antar-muka user. Sehingga masing-masing software tidak perlu lagi melakukan tugas-tugas inti umum tersebut, karena dapat dilayani dan dilakukan oleh Sistem Operasi. Bagian kode yang melakukan tugas-tugas inti dan umum tersebut dinamakan dengan “kernel” suatu Sistem Operasi. Biasanya, istilah Sistem Operasi sering ditujukan kepada semua software yang masuk.
Kalau sistem komputer terbagi dalam lapisan-lapisan, maka Sistem Operasi adalah penghubung antara lapisan hardware dan lapisan software. Lebih jauh daripada itu, Sistem Operasi melakukan semua tugas-tugas penting dalam komputer, dan menjamin aplikasi-aplikasi yang berbeda dapat berjalan secara bersamaan dengan lancar. Sistem Operasi menjamin aplikasi software lainnya dapat menggunakan memori, melakukan input dan output terhadap peralatan lain, dan memiliki akses kepada sistem file. Apabila beberapa aplikasi berjalan secara bersamaan, maka Sistem Operasi mengatur skedule yang tepat, sehingga sedapat mungkin semua proses yang berjalan mendapatkan waktu yang cukup untuk menggunakan prosesor (CPU) serta tidak saling mengganggu.
Dalam banyak kasus, Sistem Operasi menyediakan suatu pustaka dari fungsi-fungsi standar, dimana aplikasi lain dapat memanggil fungsi-fungsi itu, sehingga dalam setiap pembuatan program baru, tidak perlu membuat fungsi-fungsi tersebut dari awal.
Sistem Operasi secara umum terdiri dari beberapa bagian:
1.Mekanisme Boot, yaitu meletakkan kernel ke dalam memory
2.Kernel, yaitu inti dari sebuah Sistem Operasi
3.Command Interpreter atau shell, yang bertugas membaca input dari pengguna
4. Pustaka-pustaka, yaitu yang menyediakan kumpulan fungsi dasar dan standar yang dapat dipanggil oleh aplikasi lain
5.Driver untuk berinteraksi dengan hardware eksternal, sekaligus untuk mengontrol mereka.
Sebagian Sistem Operasi hanya mengizinkan satu aplikasi saja yang berjalan pada satu waktu, tetapi sebagian besar Sistem Operasi baru mengizinkan beberapa aplikasi berjalan secara simultan pada waktu yang bersamaan. Sistem Operasi seperti itu disebut sebagai Multi-tasking Operating System. Beberapa Sistem Operasi berukuran sangat besar dan kompleks, serta inputnya tergantung kepada input pengguna, sedangkan Sistem Operasi lainnya sangat kecil dan dibuat dengan asumsi bekerja tanpa intervensi manusia sama sekali. Tipe yang pertama sering disebut sebagai Desktop OS, sedangkan tipe kedua adalah Real-Time OS
Prosesor mengeksekusi program-program komputer. Prosesor adalah sebuah chip dalam sistem komputer yang menjalankan instruksi-instruksi program komputer. Dalam setiap detiknya prosesor dapat menjalankan jutaan instruksi.
Program adalah sederetan instruksi yang diberikan kepada suatu komputer. Sedangkan proses adalah suatu bagian dari program yang berada pada status tertentu dalam rangkaian eksekusinya. Di dalam bahasan Sistem Operasi, kita lebih sering membahas proses dibandingkan dengan program. Pada Sistem Operasi modern, pada satu saat tidak seluruh program dimuat dalam memori, tetapi hanya satu bagian saja dari program tersebut. Sedangkan bagian lain dari program tersebut tetap beristirahat di media penyimpan disk. Hanya pada saat dibutuhkan saja, bagian dari program tersebut dimuat di memory dan dieksekusi oleh prosesor. Hal ini sangat menghemat pemakaian memori.
Beberapa sistem hanya menjalankan satu proses tunggal dalam satu waktu, sedangkan yang lainnya menjalankan multi-proses dalam satu waktu. Padahal sebagian besar sistem komputer hanya memiliki satu prosesor, dan sebuah prosesor hanya dapat menjalankan satu instruksi dalam satu waktu. Maka bagaimana sebuah sistem prosesor tunggal dapat menjalankan multi-proses? Sesungguhnya pada granularity yang sangat kecil, prosesor hanya menjalankan satu proses dalam satu waktu, kemudian secara cepat ia berpindah menjalankan proses lainnya, dan seterusnya. Sehingga bagi penglihatan dan perasaan pengguna manusia, seakan-akan prosesor menjalankan beberapa proses secara bersamaan.
Setiap proses dalam sebuah sistem operasi mendapatkan sebuah PCB (Process Control Block) yang memuat informasi tentang proses tersebut, yaitu: sebuah tanda pengenal proses (Process ID) yang unik dan menjadi nomor identitas, status proses, prioritas eksekusi proses dan informasi lokasi proses dalam memori. Prioritas proses merupakan suatu nilai atau besaran yang menunjukkan seberapa sering proses harus dijalankan oleh prosesor. Proses yang memiliki prioritas lebih tinggi, akan dijalankan lebih sering atau dieksekusi lebih dulu dibandingkan dengan proses yang berprioritas lebih rendah. Suatu sistem operasi dapat saja menentukan semua proses dengan prioritas yang sama, sehingga setiap proses memiliki kesempatan yang sama. Suatu sistem operasi dapat juga merubah nilai prioritas proses tertentu, agar proses tersebut akan dapat memiliki kesempatan lebih besar pada eksekusi berikutnya (misalnya: pada proses yang sudah sangat terlalu lama menunggu eksekusi, sistem operasi menaikkan nilai prioritasnya).
(sumber :http://radensomad.com)

 Java - Programming Language
Java - Programming Language
 TURUNAN
TURUNAN


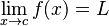
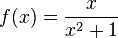
 0.4
0.4 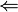
 .
. 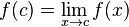 ,
,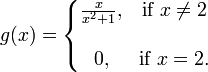
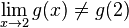 ;
; 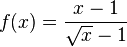

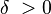
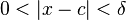
 .
.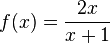 .
.

