Misalkan x dan y adalah bilangan real di mana y adalah fungsi dari x, yaitu y = f(x). Salah satu dari jenis fungsi yang paling sederhana adalah fungsi linear. Ini adalah grafik fungsi dari garis lurus. Dalam kasus ini, y = f(x) = m x + c, di mana m dan c adalah bilangan real yang tergantung pada garis mana grafik tersebut ditentukan. m disebut sebagai kemiringan dengan rumus:
di mana simbol Δ (delta) memiliki arti "perubahan nilai". Rumus ini benar adanya karena
- y + Δy = f(x + Δx) = m (x + Δx) + c = m x + c + m Δx = y + mΔx.
Diikuti pula Δy = m Δx.
Namun, hal-hal di atas hanya berlaku kepada fungsi linear. Fungsi nonlinear tidak memiliki nilai kemiringan yang pasti. Turunan dari f pada titik x adalah pendekatan yang paling baik terhadap gagasan kemiringan f pada titik x, biasanya ditandai dengan f'(x) atau dy/dx. Bersama dengan nilai f di x, turunan dari f menentukan pendekatan linear paling dekat, atau disebut linearisasi, dari f di dekat titik x. Sifat-sifat ini biasanya diambil sebagai definisi dari turunan.
Sebuah istilah yang saling berhubungan dekat dengan turunan adalah diferensial fungsi.
Garis singgung pada (x, f(x))
Bilamana x dan y adalah variabel real, turunan dari f pada x adalah kemiringan dari garis singgung grafik f' di titik x. Karena sumber dan target dari f berdimensi satu, turunan dari f adalah bilangan real. Jika x dan y adalah vektor, maka pendekatan linear yang paling mendekati grafik f tergantung pada bagaimana f berubah di beberapa arah secara bersamaan. Dengan mengambil pendekatan linear yang paling dekat di satu arah menentukan sebuah turunan parsial, biasanya ditandai dengan ∂y/∂x. Linearisasi dari f ke semua arah secara bersamaan disebut sebagai turunan total. Turunan total ini adalah transformasi linear, dan ia menentukan hiperbidang yang paling mendekati grafik dari f. Hiperbidang ini disebut sebagai hiperbidang oskulasi; ini secara konsep sama dengan mengambil garis singgung ke semua arah secara bersamaan.
sumber : http://wapedia.mobi/id/
sumber : http://wapedia.mobi/id/

 TURUNAN
TURUNAN
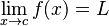
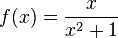
 0.4
0.4 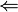
 .
. 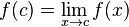 ,
,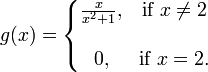
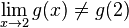 ;
; 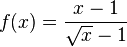

 .
. .
.

 SEJARAH KALKULUS
SEJARAH KALKULUS